HienHau: ĐỊNH LÝ THALES VÀ ỨNG DỤNG ĐO ĐẠC

"Làm thế nào để đo chiều cao của kim tự tháp, chiều cao của ngọn núi hay đo chiều rộng của một con sông".

Từ xa xưa, con người đã biết vận dụng những kiến thức toán học vào việc đo đạc, làm cho công việc phức tạp trở nên đơn giản hơn rất nhiều. Một trong những công cụ đo đạc rất hữu ích mà con người đã phát minh ra đó là định lý Thales, mang tên nhà toán học người Hy Lạp sống ở khoảng thế kỷ thứ 6 TCN.

Trong tam giác định lý Thales được phát biểu như sau:

“Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo ra những đoạn thẳng tương ứng tỷ lệ”.

Ta hiểu định lý trên một cách cụ thể như sau:

Nếu ABC là một tam giác cho trước, đường thẳng d song song với cạnh BC và cắt AB tại M, cắt AC tại N thì ta sẽ có các tỷ lệ thức sau:

Ở chiều ngược lại, “nếu tỷ lệ thức (*) thoả mãn thì đường thẳng d song song với cạnh BC”. Điều này thường gọi là định lý đảo của định lý Thales.

Đây là một định lý có rất nhiều ứng dụng thực tế, việc chứng minh cũng rất đơn giản. Chỉ cần những kiến thức cơ bản của lớp 5 là ta có thể chứng minh được nó.

😄

Thật vậy, trước hết ta sẽ chứng minh chiều thuận của định lý, tức là chứng minh nếu d song song với BC và cắt AB tại M cắt AC tại N thì ta có tỷ lệ thức (*).

Do tam giác AMN và tam giác ABN có chung đường cao hạ từ N nên.

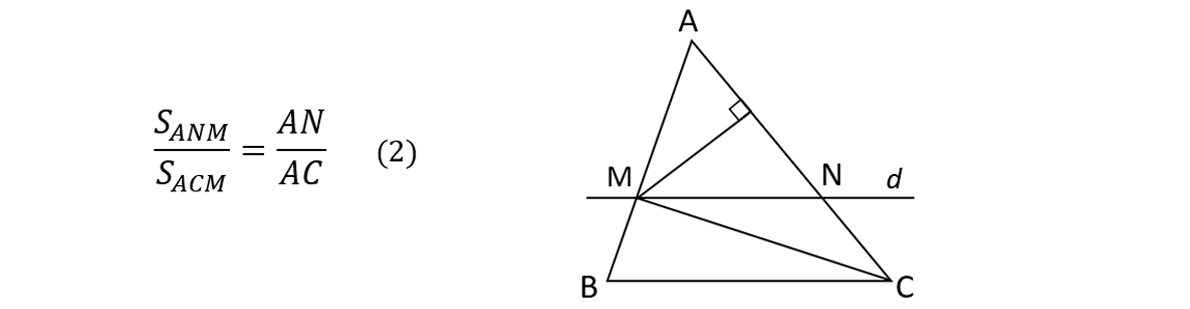
Tương tự, tam giác ANM và ACM có trung đường cao hạ từ M nên.

Do MN // BC nên

Từ (1), (2) và (3)

Bây giờ ta kẻ đường thẳng t đi qua N và song song với AB, t cắt BC tại E.

Ta có BMNE là hình bình hành nên MN = BE

Chứng minh theo cách ở trên ta sẽ có:

Như vậy, từ (4) và (5) ta có tỷ lệ thức (*)

Với chiều ngược lại, giả sử ta có tỷ lệ thức:

Ta sẽ chứng minh MN // BC.

Thật vậy, theo (1), (2) và

Và do 2 tam giác BMN và CNM có chung cạnh đáy MN nên các đường cao hạ từ B và C bằng nhau suy ra BC song song MN (đpcm)

Mở rộng định lý Thales cho 2 tam giác đồng dạng.

Giả sử có 2 tam giác ABC và MNE là đồng dạng với nhau.

Đặt góc M trùng vào góc A thì ta sẽ có NE // BC và do đó.

Cho 2 đường thẳng d và t song song với nhau. Gọi O là điểm bất kỳ không nằm trên d và t khi đó những đường thẳng đi qua O cắt d và t sẽ tạo ra các đoạn thẳng tỷ lệ.